L'essenziale del linguaggio Java per realizzare l'insieme di Mandelbrot e di Julia.


Capitolo 6:
Come elevare la Z della formula (Z² + c)fino alla XXX ^a potenza.

Sappiamo che la formula dell'insieme di mandelbrot è (Z² + c).
Ma cosa succede se aumentiamo il valore della potenza, se dalla seconda la portiamo alla terza, alla quarta, alla quinta o adirittura fino alla trentesima potenza e come appariranno gli eventuali in grandimenti.
In questo applet vedremo come ottenere tutto questo, intanto vediamo qualche immagine d'esempio delle varie applicazioni della formula.
Nei disegni la potenza della formula e indicata dalla quarta barra di scorrimento "power of".

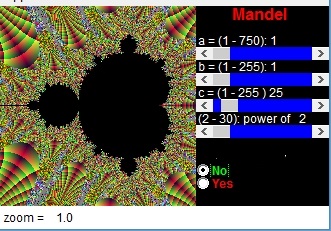
Questa e l'usuale formula utilizzata fin'ora (Z² + c).

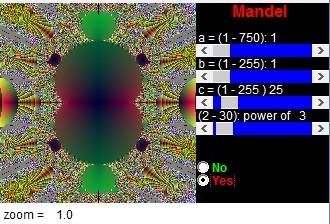
In questa immagine abbiamo ( Z³ +c).

In questa immagine abbiamo

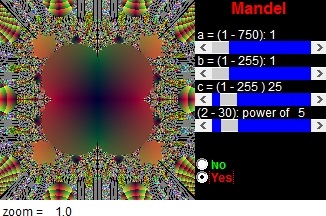
Qui abbiamo

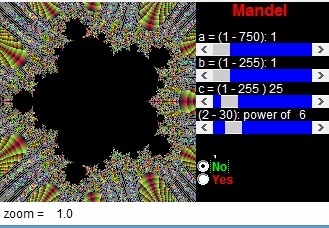
Qui abbiamo (Z^{6 +c)}

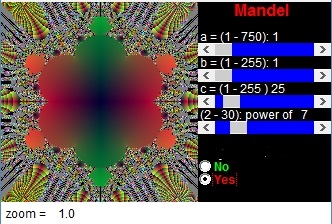
Qui abbiamo (Z^{7 +c).}

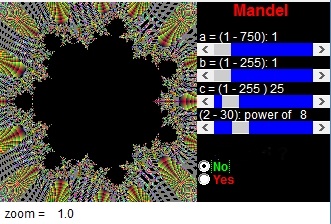
Qui abbiamo (Z^{8 +c).}

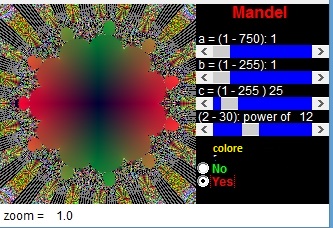
Per ragioni spazio qui saltiamo alla (Z^{12 +c).}

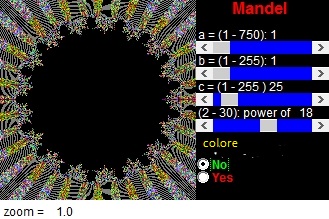
Mentre qui andiamo alla 18 potenza.

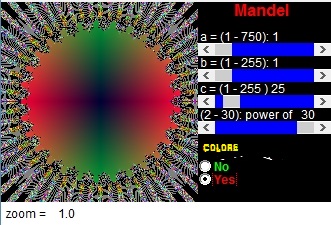
Mentre qui siamo alla nostra ultima potenza, la trentesima

Questo sotto è il listato di mandelbrot che ci permette di variare l'esponente della formula,
la parte nuova è tutta commentata

Potete selezionare il testo, copiarlo e incollarlo all'interno di un applet che chiamerete Mand_Power2 compilatelo ed eseguitelo, dovreste vedere delle immagine simili a queste sopra

Come aumentare l'esponente della formula.

(Z²)=(a+bi)*(a+bi)
reale = a*a- b*b;
immaginaria = 2*a*b;

Questa è la formula (Z²) in forma algebrica che abbiamo già visto nel precedente programma.

Per la formula (Z³) =

(a+bi)* (a+bi)*(a+bi)
abbiamo per la parte
reale= (a^3-3*a*b^2) = (a*a *a - 3*a*b*b)
per quella
immaginaria = (3*a^2*b-b^3) = (3*a*a*b - b*b*b)
Questa per la terza potenza.

Per la formula (Z⁴ ;) =
(a+bi)* (a+bi)*(a+bi)*(a+bi)
reale= (a^4-6*a^2*b^2+b^4) = (a*a*a*a- 6*a*a*b*b+ b*b*b*b)
immaginaria = (4*a^3*b-4*a*b^3)= (4*a*a*a*b- 4*a*b*b*b)
Già alla quarta potenza la formula comincia a diventare lunga.

Con (Z⁵) abbiamo
(a+bi)* (a+bi)*(a+bi)*(a+bi)*(a+bi)
reale= ( a^5 – 10*a^3*b^2+5*a *b^4)= (a*a*a*a*a- 10*a*a*a*b*b+ 5*a*b*b*b*b)
immaginaria = ( 5*a^4*b - 10*a^2 *b^3+ b^5)= (5*a*a*a*a*b- 10*a*a*b*b*b+ b*b*b*b*b)

Come potete vedere, per elevare alla seconda potenza, il codice è abbastanza semplice, ma dopo il quinto esponente la formula diventa davvero troppo lunga, immaginate la quantità di codice per elevare alla potenza trentesima, per fortuna, ho trovato un modo più veloce per risolvere il problema con poche righe di codice in più del solito algoritmo.

Questo è un ingran
dimento dell'insieme
di Mandelbrot Z³

Questo è un ingran
dimento dell'insieme
di Mandelbrot Z⁴

Questo è un ingran
dimento dell'insieme
di Mandelbrot Z⁵

Altri esempi dell'insieme di mandelbrot.
Questo è un ingran
dimento dell'insieme di Mandelbrot

Mentre questo è un ingran
dimento di